SDUTOJ1730（记忆化搜索）：数字三角形

SDUTOJ1730（记忆化搜索）：数字三角形

========================

题目如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
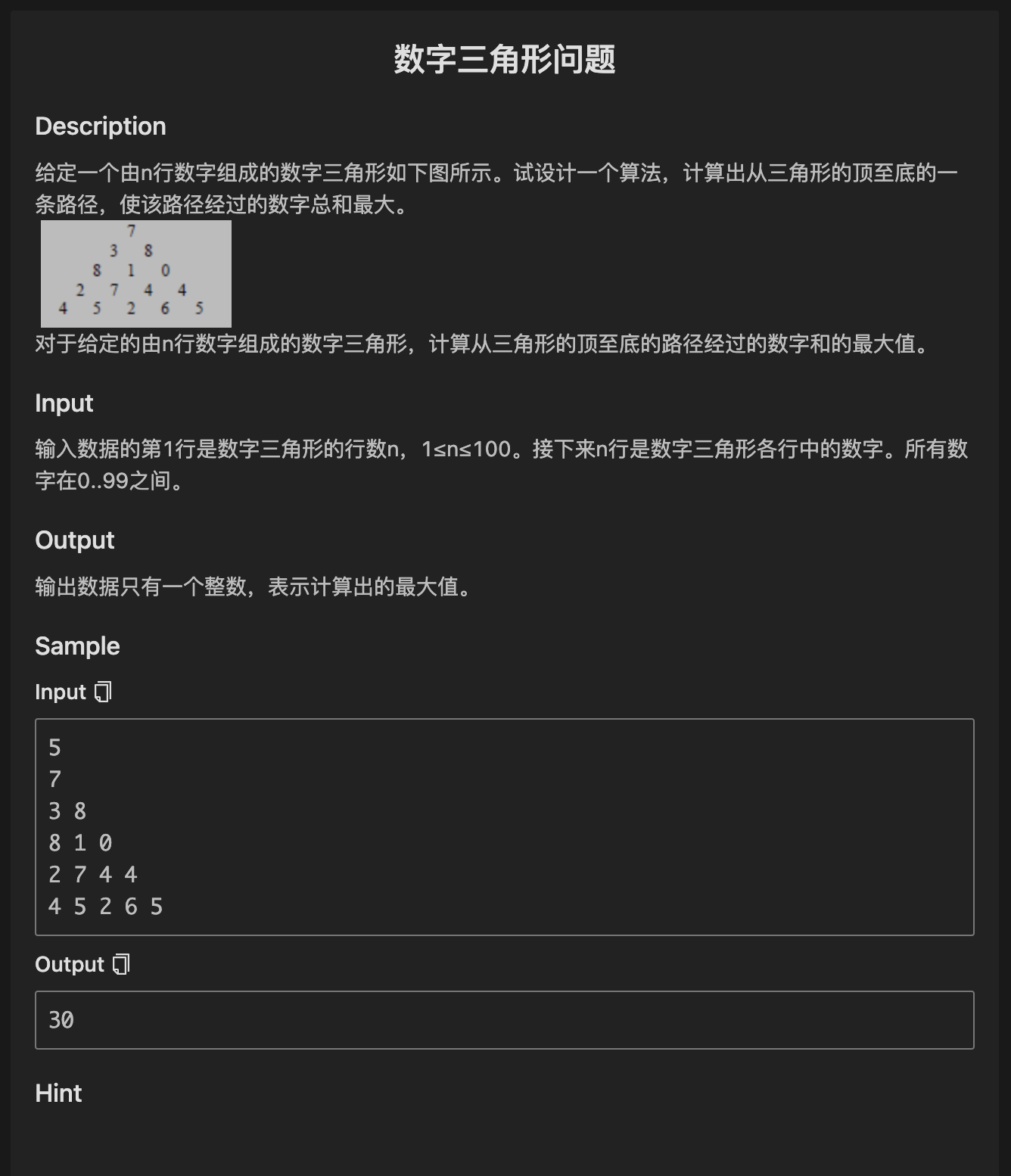
数字三角形问题
Description
给定一个由n行数字组成的数字三角形如下图所示。试设计一个算法，计算出从三角形的顶至底的一条路径，使该路径经过的数字总和最大。
 
对于给定的由n行数字组成的数字三角形，计算从三角形的顶至底的路径经过的数字和的最大值。
Input
输入数据的第1行是数字三角形的行数n，1≤n≤100。接下来n行是数字三角形各行中的数字。所有数字在0..99之间。
Output
输出数据只有一个整数，表示计算出的最大值。
Sample
Input 
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Output 
30

我的代码

1
//题目较为简单，记录即可。

心得： 这是一道比较经典的动规及记忆化搜索题，难度中等。

解法一

数组递推

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <algorithm>
#include <bitset>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
using namespace std;
const int N=111;
int dp[N][N],a[N][N];

int main(int argc, char const *argv[]) {
    int n;
    int res=0;
    int i,j;
    cin>>n;
    for(i=1;i<=n;i++)
    {
        for(j=1;j<=i;j++)
        {
            cin>>a[i][j];
        }
    }
    dp[1][1]=a[1][1];
    for( i=2;i<=n;i++)
    {
        dp[i][1]=dp[i-1][1]+a[i][1];
        dp[i][i]=dp[i -1][i- 1] +a[i][i];  //边界情况
        for(j=2;j<i;j++){
            dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+a[i][j];  
            }
    }
    for(int i=1;i<=n;i++) res=max(res,dp[n][i]);  //求各个路径结果的最大值
    cout<<res;
    return 0;
}

解法二（深度优先，超时解法）

1
2
3
4
5
6
7
8
void dfs(x,y,c){   //c用来记录累加的结果
    if(x==n-1){
        if(c>ans) ans=c   //取最后累加结果的最大值  ans用来存储
        return ;
    } 
    dfs(x+1,y,c+a[x+1][y]);
    dfs(x+1,y+1,c+a[x+1][y+1]);
}

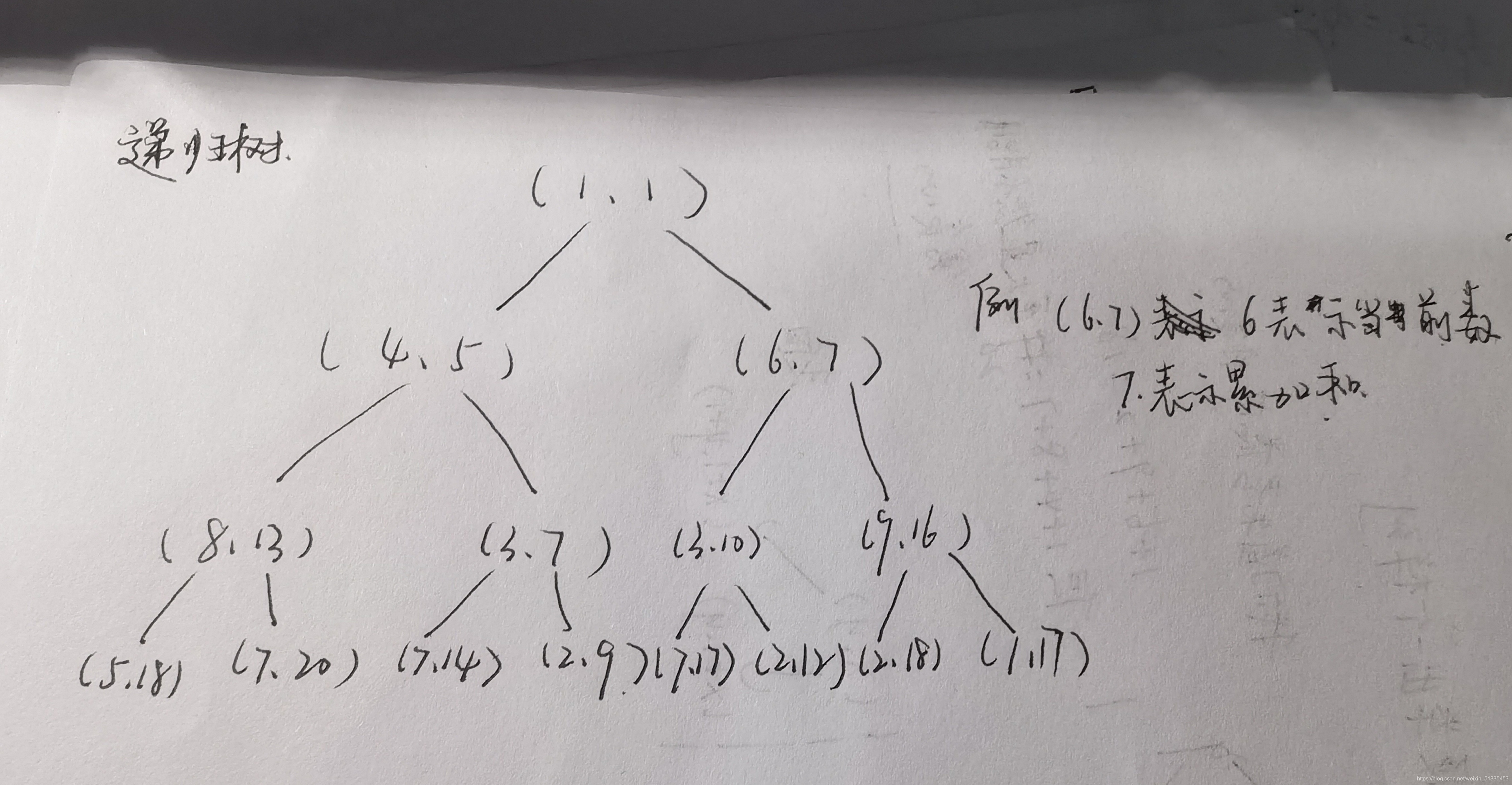
通过深度优搜索（dfs）画出递归树来模拟执行过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>  //超时算法

using namespace std;
const int N=1e5+10;
int a[N][N];
int ans=0;

void dfs(int x,int y,int c,int n){
    if(x==n-1){
        if(c>ans) ans=c;
        return ;
    }
    dfs(x+1,y,c+a[x+1][y],n);
    dfs(x+1,y+1,c+a[x+1][y+1],n);
}

int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
            cin>>a[i][j];
        }
    } 
    dfs(0,0,a[0][0],n);
    cout<<ans<<endl;
    return 0;
 }

深度优先搜索其实质就是二叉树的先序遍历（没学过的直接用递推或者递归的算法求解）
我们发现有些点被重复搜索了好几遍这就耗费了很多的时间，实际上也是这样的这种算法的时间复杂度为O(2^n)指数级复杂度肯定要超时的，这时我们就希望有一种算法能够在第一次搜索的过程中就记录下来之后用的时候就不需要继续搜索了，这就引出我们的记忆化搜索。

解法三（记忆化搜索）

我们发现从上向下累加和是不能重复的，但从下向下的累加是可以重复用的这也是记忆化搜索的前提。记忆化搜索：对递归树做了剪枝，搜索过的子树不再重复搜索，直接返回储存值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <iostream>

using namespace std;
const int N=1500;
int a[N][N];
int f[N][N];   //记录从上到下的累加和 
int ans=0;
int n;

int dfs(int x,int y){
    //记忆搜索， 避免进一步递归 
    if(f[x][y]!=0) return f[x][y];   //由于开全局数组初始化都为0不为零就相当于已经搜索过就记录下来 
    if(x==n-1)   //边界条件 
    f[x][y]=a[x][y];
    else
    f[x][y]=a[x][y]+max(dfs(x+1,y),dfs(x+1,y+1));
    return f[x][y];
}


int main()
{
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<=i;j++){
            cin>>a[i][j];
        }
    } 
    dfs(0,0);
    cout<<f[0][0]<<endl;
    return 0;
 }

其实找准动态规划与贪心的区别后，理解起来就不那么难了，动态规划的关键词就是状态和状态转移方程，找好这两个问题就可以解决了，然后dfs深搜，和记搜有时候牵扯到后面的二叉树，先不用理解的太深，代码就多一行记住后以后就会慢慢的理解了。其实递推的方法求数塔问题是也是有用数组记录了值，和记忆化搜索有些相似，大家可以结合理解，加油！
题目链接：https://acm.sdut.edu.cn/onlinejudge3/problems/1730