动态规划之状态压缩

动态规划之状态压缩摘录

========================

一、概述

1.状态压缩

状态压缩就是使用某种方法，简明扼要地以最小代价来表示某种状态，通常是用一串01数字（二进制数）来表示各个点的状态。这就要求使用状态压缩的对象的点的状态必须只有两种，0 或 1；当然如果有三种状态用三进制来表示也未尝不可。

2.使用条件

从状态压缩的特点来看，这个算法适用的题目符合以下的条件：

  • 解法需要保存一定的状态数据（表示一种状态的一个数据值），每个状态数据通常情况下是可以通过2进制来表示的。这就要求状态数据的每个单元只有两种状态，比如说棋盘上的格子，放棋子或者不放，或者是硬币的正反两面。这样用0或者1来表示状态数据的每个单元，而整个状态数据就是一个一串0和1组成的二进制数。
  • 解法需要将状态数据实现为一个基本数据类型，比如int，long等等，即所谓的状态压缩。状态压缩的目的一方面是缩小了数据存储的空间，另一方面是在状态对比和状态整体处理时能够提高效率。这样就要求状态数据中的单元个数不能太大，比如用int来表示一个状态的时候，状态的单元个数不能超过32（32位的机器），所以题目一般都是至少有一维的数据范围很小。

3.状压DP

状压DP，顾名思义，就是使用状态压缩的动态规划。

动态规划问题通常有两种，一种是对递归问题的记忆化求解，另一种是把大问题看作是多阶段的决策求解。这里用的便是后一种，这带来一个需求，即存储之前的状态，再由状态及状态对应的值推演出状态转移方程最终得到最优解。

二、位运算

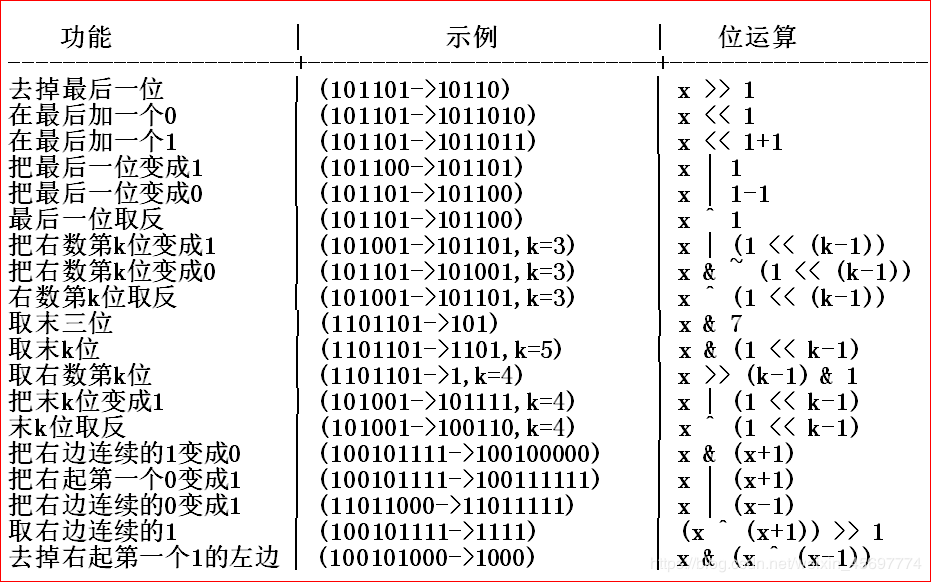
一般基础的状压就是将一行的状态压成一个数，这个数的二进制形式反映了这一行的情况。由于使用二进制数来保存被压缩的状态，所以要用到神奇的二进制位运算操作，将一个十进制数转成二进制进行位运算操作再转回十进制数。包括：

  • 按位与&（有0为0，其实就是且）
  • 按位或|（有1为1，其实就是或）
  • 按位取反~（注意负数补码的符号，最前面的第一位是1）
  • 异或^（相同为0，不同为1）
  • 左移<<
  • 右移>>

常见操作：

  • 判断x是奇数还是偶数：(x&1)==0
  • x乘以一个2的n次方的数：x<<n
  • x除以一个2的n次方的数：x>>n
  • 消去x最后一位的1：x&(x-1)
  • 求x的相反数： (x-1)或者x+1
  • x的异或操作：~x = -x-1
  • 把x从右边数第n位变1：x|(1<<(n-1))（n从1开始）
  • 把x从右边数第n位变0：x&(~(1<<(n-1)))（n从1开始）
  • 取x最后n位的值：x&((1<<n)-1)
  • 取x前n位的值，后面的全部置为0：x & (~((1 << (32 - n)) - 1))
  • 只保留x右边第一个1，其他的全部置为0：x & (-x) 或 x & ~(x - 1)
  • 判断x的第n位是偶数还是奇数：(x & (1 << (n - 1))) == 0
  • 求x的绝对值：(n ^ (n >> 31)) - (n >> 31) 或 (x >> 31) == 0 ? x : (~x + 1) 或 (x + (x >> 31)) ^ (x >> 31)
  • 求两个数的最大数：(x & ((y - x) >> 31)) | (y & (~(y - x) >> 31))
  • 返回x的符号：(i >> 31) | (-i >>> 31)（正数为1，负数为-1）
  • 两数相加：(x | y) + (x & y) 或 (x ^ y) + ((x & y) << 1)
  • 两数相减：(x & y) - (x & y)
  • 求两数的平均数：(x & y) + ((x ^ y) >> 1) 或 (x + y) >> 1
  • 判断一个数是不是2的次幂：(x != 0) && (x & (x - 1)) == 0
  • x对2的n次方求余：x & (2^n - 1)（这里的^是幂的次方）
  • 判断x和y的符号是否相同：(a ^ b) >= 0
  • if(x == a) x = b; if(x == b) x = a：用异或运算符：x = a ^ b ^ x

初试化状态的时候要看清条件，什么要，什么不要。
一般情况下要预处理前k行（k由题目定）。
Dp时题目给的条件和fit函数、state数组都要检查。

最最重要的一点：

位反（~ ) > 算术 > 位左移、位右移 > 关系运算
>位与 > 位或 > 位异或 > 逻辑运算

所以一般位运算最好打括号。

三、例题引入

【例1】填满棋盘

有一个NM(N<=5,M<=1000)的棋盘，现在有12及2*1的小木块无数个，要盖满整个棋盘，有多少种方式？答案只需要mod1,000,000,007即可。

例如：对于一个22的棋盘，有两种方法，一种是使用2个12的，一种是使用2个2*1的。

【算法分析】

在这道题目中,N和M的范围本应该是一样的，但实际上，N和M的范围却差别甚远，对于这种题目，首先应该想到的就是，正确算法与这两个范围有关！N的范围特别小，因此可以考虑使用状态压缩动态规划的思想，请看下面的图：

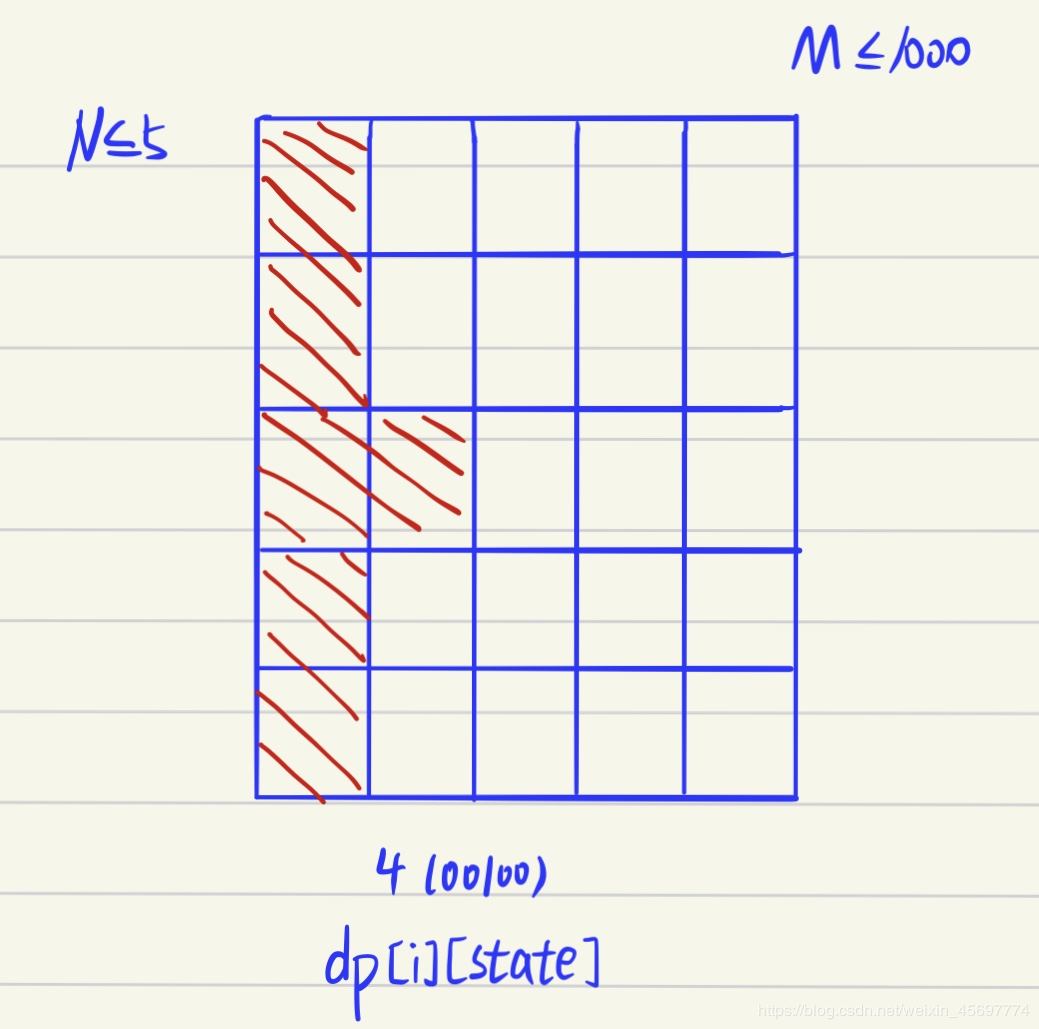
本思路来自博客，不过原博没有图，我帮他补个图，再优化一下内容。

假设第一列已经填满，则第二列的摆设方式，只与第一列对第二列的影响有关。同理，第三列的摆设方式也只与第二列对它的影响有关。那么，使用一个长度为NN的二进制数statestate来表示这个影响，例如：4(00100)就表示了图上第二列的状态。

因此，本题的状态可以这样表示：

dp[i][state]表示该填充第 ii 列，第 i-1i−1 列对它的影响是 statestate 的时候的方法数。i<=M,0<=state<2^Ni<=M,0<=state<2
N

对于每一列，情况数也有很多，但由于 NN 很小，所以可以采取搜索的办法去处理。对于每一列，搜索所有可能的放木块的情况，并记录它对下一列的影响，之后更新状态。状态转移方程如下：

dp[i][state]=∑dp[i-1][pre] 每一个prepre可以通过填放成为statestate

对于每一列的深度优先搜索，写法如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//第i列，枚举到了第j行，当前状态是state，对下一列的影响是nex
void dfs(ll i,ll j,ll state,ll nex)
{
    if(j==n)//最后一行
    {
        dp[i+1][nex]+=dp[i][state];
        dp[i+1][nex]%=mod;
        return;
    }
    //如果这个位置（第j行）已经被上一列给站了（state的第j位为1），所以就直接跳过
    if(state&(1<<j)>0)
        dfs(i,j+1,state,nex);
    //如果这个位置是空的，那么就尝试放一个1*2的棋子
    if(state&(1<<j)==0)
        dfs(i,j+1,state,nex|(1<<j));//（使nex的第j位变成1）
    //如果这个位置以及下一行都空的，那么就放一个2*1的棋子并直接跳到下下行
    if(j+1<n&&state&(1<<j)==0&&state&(1<<j+1)==0)//注意要特判第j行下面是否还有一行
        dfs(i,j+2,state,nex);
    return;
}

最终，答案就是dp[M+1][0]。
完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=2000+7;
const ll mod=1000000007;
ll n,m;
ll dp[N][N];//dp[i][state]; 铺满前i-1列的所有方案数
//第i列，枚举到了第j行，当前状态是state，对下一列的影响是nex
void dfs(ll i,ll j,ll state,ll nex)
{
    if(j==n)//最后一行
    {
        dp[i+1][nex]+=dp[i][state];//nex一直接受前面的变化直到最后一行当前的可能性已经遍历完了就+上即可
        dp[i+1][nex]%=mod;
        return;
    }
 
    //如果这个位置（第j行）已经被上一列给占了（state的第j位为1），所以就直接跳过
    if(((1<<j)&state)>0)
        dfs(i,j+1,state,nex);//不会对下一列有什么影响
 
    //如果这个位置是空的，那么就尝试放一个1*2的棋子
    if(((1<<j)&state)==0)
        dfs(i,j+1,state,nex|(1<<j));//（使nex的第j位变成1）横着放一个1*2的棋子会对下一列造成影响
 
    //如果这个位置以及下一行都空的，那么就放一个2*1的棋子并直接跳到下下行
    if(j+1<n&&((1<<j)&state)==0&&((1<<(j+1))&state)==0)//注意要特判第j行下面是否还有一行,以及要加上足够的括号以免因为位运算的优先级问题而导致出bug
        dfs(i,j+2,state,nex);//不会对下一列造成影响
 
    return;
}
int main()
{
    while(~scanf("%lld %lld",&n,&m))
    {
        if(n==0&&m==0)break;
        memset(dp,0,sizeof dp);
        dp[1][0]=1;//注意初始化
        for(int i=1;i<=m;++i)//一共m列//枚举第i列 -> 影响第i+1列
        {
            //注意1<<n结果是二进制，到for循环中会转换成十进制计算，这里最多也就是2的5次方，即32，可别以为是十进制的100000。
            //如下为遍历情况：
//            *0 *0 *0 *0     *1 *1 *1 *1
//            *0 *0 *0 *0     *1 *1 *1 *1
//            *0 *0 *0 *0 ... *1 *1 *1 *1
//            *0 *0 *1 *1     *0 *0 *1 *1
//            *0 *1 *0 *1     *0 *1 *0 *1
            for(int j=0;j<(1<<n);++j)//到2^n，遍历一遍，二进制会把所有填充的情况都列举一遍
            {
                if(dp[i][j])//如果存在方案数 -> 则可以推广到i+1列
                    dfs(i,0,j,0);
            }
        }
        printf("%lld\n",dp[m+1][0]);
    }
    return 0;
}

要注意多加几个括号，能加就加，以免因为位运算的优先级问题而导致出bug。

【例2】最小总代价（Vijos-1456）

题目描述：

n个人在做传递物品的游戏,编号为1-n。

游戏规则是这样的：开始时物品可以在任意一人手上，他可把物品传递给其他人中的任意一位；下一个人可以传递给未接过物品的任意一人。

即物品只能经过同一个人一次，而且每次传递过程都有一个代价；不同的人传给不同的人的代价值之间没有联系；

求当物品经过所有n个人后，整个过程的总代价是多少。

输入格式：

第一行为n,表示共有n个人（16>=n>=2）；

以下为n*n的矩阵，第i+1行、第j列表示物品从编号为i的人传递到编号为j的人所花费的代价，特别的有第i+1行、第i列为-1（因为物品不能自己传给自己），其他数据均为正整数(<=10000)。

(对于50%的数据，n<=11)。

输出格式：

一个数，为最小的代价总和。

输入样例：

2

-1 9794

2724 –1

输出样例：

2724

【算法分析】

看到2<=n<=16，应想到此题和状态压缩dp有关。每个人只能够被传递一次，因此使用一个n位二进制数state来表示每个人是否已经被访问过了。但这还不够，因为从这样的状态中，并不能清楚地知道现在物品在谁 的手中，因此，需要在此基础上再增加一个状态now，表示物品在谁的手上。

dp[state][now]表示每个人是否被传递的状态是state，物品在now的手上的时候，最小的总代价。

初始状态为：dp[1<<i][i]=0；表示一开始物品在i手中。

所求状态为：min(dp[(1<<n)-1][j]); 0<=j<n

状态转移方程是：

dp[state][now]=min(dp[pre][t]+dist[now][t])；

pre表示的是能够到达state这个状态的一个状态，t能够传递物品给now且只有二进制下第t位与state不同。

状态的大小是O((2n)*n)，转移复杂度是O(n)。总的时间复杂度是O((2n)nn)。

【代码实现】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
/*
ID:shijieyywd
PROG:Vijos-1456
LANG:c++
*/
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
 
#define MAXN 20
#define INF 0x3f3f3f3f
 
using namespace std;
 
int n;
int edges[MAXN][MAXN];
int dp[65546][MAXN];
 
int min(int a, int b) 
{
	if (a == -1) return b;
	if (b == -1) return a;
	return a < b ? a : b;
}
 
int main() {
	freopen("p1456.in", "r", stdin);
	scanf("%d", &n);
	int t;
	for (int i = 0; i < n; i++) 
	{
		for (int j = 0; j < n; j++) 
		{
			scanf("%d", &edges[i][j]);
		}
	}
	memset(dp, -1, sizeof(dp));
	for (int i = 0; i < n; i++) 
	{
		dp[1 << i][i] = 0;
	}
	int ans = -1;
	for (int i = 0; i < 1 << n; i++) 
	{
		for (int j = 0; j < n; j++) 
		{
			if (dp[i][j] != -1) 
			{
				for (int k = 0; k < n; k++) 
				{
					if (!(i & (1 << k))) 
					{
						dp[i | (1 << k)][k] = min(dp[i | (1 << k)][k], dp[i][j] + edges[j][k]);
						if ((i | (1 << k)) == (1 << n) - 1) ans = min(ans, dp[i | (1 << k)][k]);
					}
				}
			}
		}
	}
	if (ans != -1)
		printf("%d\n", ans);
	else printf("0\n");
 
	return 0;
}

【例3】胜利大逃亡(续)(Hdoj-1429)

题目描述：

Ignatius再次被魔王抓走了(搞不懂他咋这么讨魔王喜欢)……

这次魔王汲取了上次的教训，把Ignatius关在一个n*m的地牢里，并在地牢的某些地方安装了带锁的门，钥匙藏在地牢另外的某些地方。刚开始Ignatius被关在(sx,sy)的位置，离开地牢的门在(ex,ey)的位置。Ignatius每分钟只能从一个坐标走到相邻四个坐标中的其中一个。魔王每t分钟回地牢视察一次，若发现Ignatius不在原位置便把他拎回去。经过若干次的尝试，Ignatius已画出整个地牢的地图。现在请你帮他计算能否再次成功逃亡。只要在魔王下次视察之前走到出口就算离开地牢，如果魔王回来的时候刚好走到出口或还未到出口都算逃亡失败。

输入格式：

每组测试数据的第一行有三个整数n,m,t(2<=n,m<=20,t>0)。接下来的n行m列为地牢的地图，其中包括:

. 代表路

  • 代表墙

@ 代表Ignatius的起始位置

^ 代表地牢的出口

A-J 代表带锁的门,对应的钥匙分别为a-j

a-j 代表钥匙，对应的门分别为A-J

每组测试数据之间有一个空行。

输出格式：

针对每组测试数据，如果可以成功逃亡，请输出需要多少分钟才能离开，如果不能则输出-1。

输入样例：

4 5 17

@A.B.

a*.*.

*..*^

c..b*

输出样例：

16

【算法分析】

初看此题感觉十分像是宽度优先搜索（BFS），但搜索的过程中如何表示钥匙的拥有情况，却是个问题。借鉴状态压缩的思想，使用一个10位的二进制数state来表示此刻对10把钥匙的拥有情况，那么，dp[x][y][state]表示到达(x,y)，钥匙拥有状况为state的最短路径。另外，需要注意到一旦拥有了某一把钥匙，那个有门的位置就如履平地了。

代码的实现方式可以采用Spfa求最短路的方式。值得一提的是，Spfa算法本来就是一种求解最短路径问题的动态规划算法，本文假设读者已经非常熟悉Spfa等基础算法，在此处不再赘述。

状态压缩dp可以出现在各种算法中，本题就是典型的搜索算法和状态压缩dp算法结合的题目。另外，很多状态压缩dp本身就是通过搜索算法实现的状态转移。

【代码实现】

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
/*
ID:shijieyywd
PROG:Hdu-1429
LANG:c++
*/
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
 
using namespace std;
 
struct Node{
	int x;
	int y;
	int step;
	int key;
	Node() {}
	Node(int a, int b, int s, int k) : x(a), y(b), step(s), key(k) {}
};
 
int n, m, t;
int arr[25][25];
int door[25][25];
int key[25][25];
int Go[4][2] = {{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
int sx, sy;
int ex, ey;
int vis[25][25][1049];
 
bool canGo(int x, int y, int k) 
{
	if (x >= 0 && x < n && y >= 0 && y < m && !arr[x][y]) 
	{
		if (vis[x][y][k]) return false;
		if ((k & door[x][y]) == door[x][y]) return true;
	}
	return false;
}
 
int bfs() {
	memset(vis, 0, sizeof(vis));
	queue<Node> q;
	Node s = Node(sx, sy, 0, 0);
	q.push(s);
	vis[sx][sy][0] = 1;
	while (!q.empty()) 
	{
		Node e = q.front();
		q.pop();
		if (e.x == ex && e.y == ey) return e.step;
		for (int i = 0; i < 4; i++) 
		{
			int nx = e.x + Go[i][0];
			int ny = e.y + Go[i][1];
			if (canGo(nx, ny, e.key)) 
			{
				Node nex = Node(nx, ny, e.step + 1, e.key | key[nx][ny]);
				vis[nx][ny][nex.key] = 1;
				q.push(nex);
			}
		}
	}
	return 0;
}
 
int main() {
	while (~scanf("%d %d %d\n", &n, &m, &t)) 
	{
		memset(arr, 0, sizeof(arr));
		memset(door, 0, sizeof(door));
		memset(key, 0, sizeof(key));
		char c;
		for (int i = 0; i < n; i++) 
		{
			for (int j = 0; j < m; j++) 
			{
				scanf("%c", &c);
				if (c == '*') arr[i][j] = 1;
				else if (c == '@') sx = i, sy = j;
				else if (c == '^') ex = i, ey = j;
				else if (c >= 'a' && c <= 'z') key[i][j] = 1 << (c - 'a');
				else if (c >= 'A' && c <= 'Z') door[i][j] = 1 << (c - 'A');
			}
			getchar();
		}
		int ans = bfs();
		if (ans < t && ans) printf("%d\n", ans);
		else printf("-1\n");
	}
	return 0;
}